$x sin (a+y)+sin acos(a+y)=0$
$sin(a+y)dx+ x(cos(a+y))dy$
$-sin asin(a+y)dy=0$
$sin(a+y)dx+ (xcos(a+y))$
$-sinasin(a+y)dy=0$
$\implies \frac{dy}{dx}=$
$\frac{sin(a+y)}{sinasin(a+y)$ $-xcos(a+y)}$
$=\frac{sin(a+y)}{sin asin(a+y)+$
$cos(a+y)$
$(\frac{sinacos(a+y)}{sin(a+y)})}$
$= \frac{sin(a+y)}{sin asin(a+y)$
$+(\frac{sinacos^{2}$
$(a+y)}{sin(a+y)})}$
$= \frac{sin^{2}(a+y)}{sin asin^{2}(a+y)$ $+ sinacos^{2}(a+y)}$
$\implies \frac{sin^{2}$
$(a+y)}{sina(sin^{2}(a+y)$
$+cos^{2}(a+y))}$
$\implies \frac{dy}{dx}=
\frac{sin^{2}(a+y)}{sin a}$


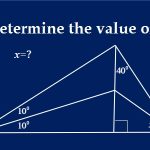
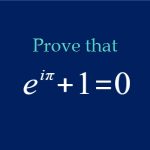
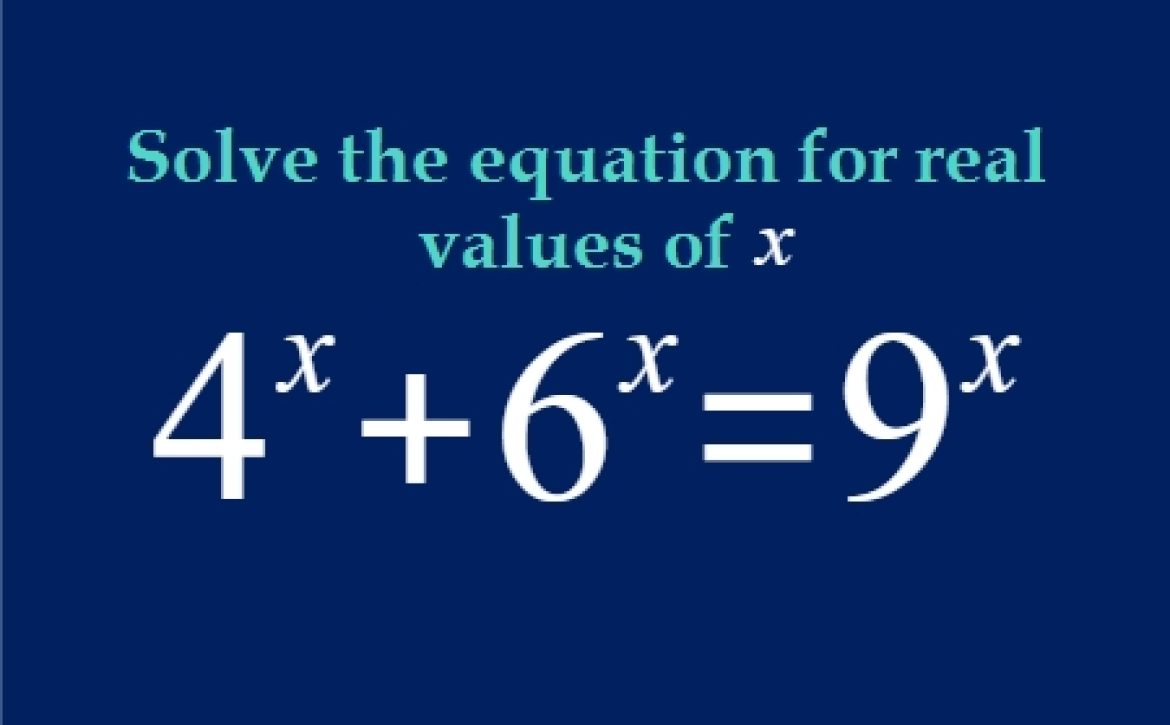

We realised we really wanted to catch a glimpse of what went on behind the scenes of the companies we looked up to. And we thought other people would want to know too.
So we decided to organise an event to share these stories. Today, we run monthly Show & Tell events and an annual conference.