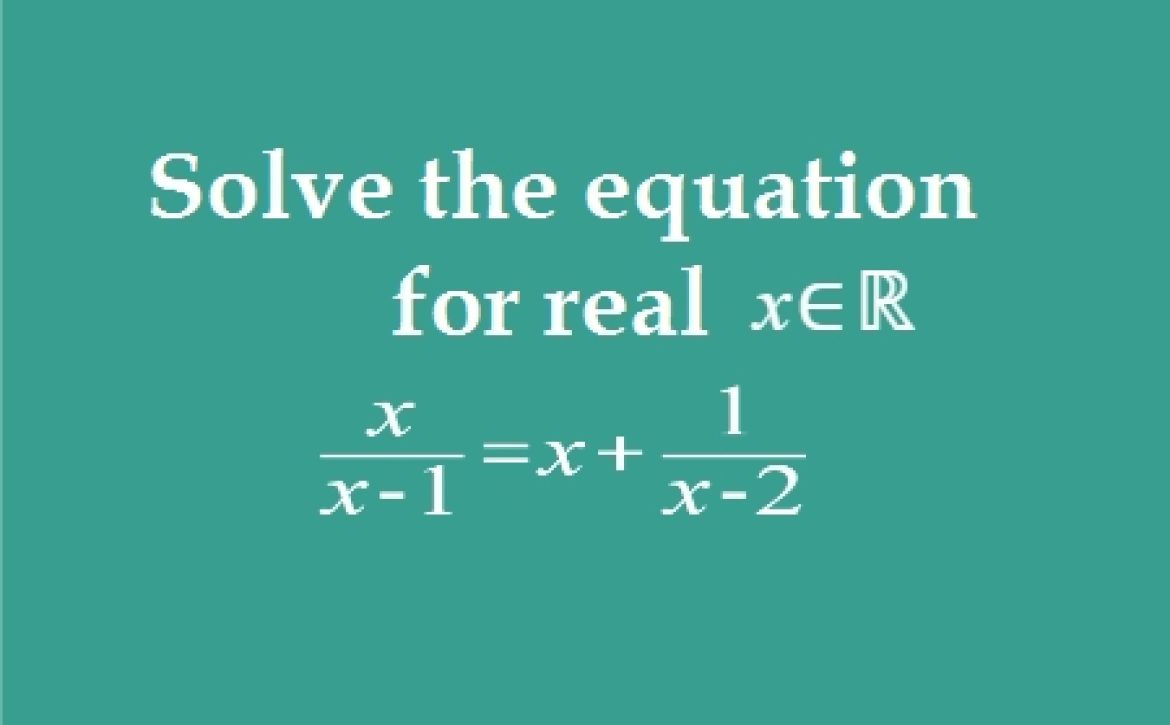
327 Views
Solve for the real value of x
$=(x+\frac{1}{x-2})(x-1)(x-2)$
$x\ne 1$ and $x\ne 2$
$\implies x(x-2)=x(x-1)(x-2)+x-1$
$\implies x^{2}-2x=x^{3}$
$-2x^{2}-x^{2}+2x+x-1$
$\implies x^{3}-4x^{2}+5x-1=0$
Now we are dealing with a cubic equation , this can be made by replacing $x$ by $y+ \frac{4}{3}$ to get rid of $x^{2} $ term, this gives
$+ 5(y+\frac{4}{3})-1=0$
$ y^{2}+3y^{2}(\frac{4}{3})+$
$3y(\frac{4}{3})+ (\frac{4}{3})^3$
$-4(y^{2}+2y(\frac{4}{3}))+(\frac{4}{3})^{2}$
$+5y+\frac{20}{3}-1=0$
$ y^{3}+4y^{2}+\frac{16y}{3}$
$+\frac{64}{27}-4y^{2}-\frac{32y}{3}$
$-\frac{64}{9}+5y+\frac{20}{3}-1=0$
$\implies y^{3}-\frac{y}{3}+\frac{25}{27}=0$
$B=\frac{25}{27}$, we get
$A-3st=0$
Here we use the larger solution , the other solution also works. This gives
$t=\frac{1}{3}\sqrt[3]{\frac{25+\sqrt[3]{69}}{2}}$ and
$s=\frac{A}{3t}=-\frac{1}{3}\sqrt[3]{\frac{2}{25+\sqrt[3]{69}}}$
Hence, the solution $x=y+\frac{4}{3}=s-t+\frac{4}{3}$
$f^{'}=3x^{2}-8x+5=(x-1)(3x-5)$
It is possible in $(\infty, 1]$ negative in $(1,\frac{5}{3})$ and possible in $\frac{5}{3}, \infty$ , since $f(t)=1$ and $f(\frac{5}{3})=\frac{23}{27}$, the function $f$ is possible in $[, \infty$ and has only one zero which is $\approx 0.24$ in $-\infty, 1$.



We realised we really wanted to catch a glimpse of what went on behind the scenes of the companies we looked up to. And we thought other people would want to know too.
So we decided to organise an event to share these stories. Today, we run monthly Show & Tell events and an annual conference.